1.3 Node degree

Recall, our definition of an undirected graph.

Definition 1: Undirected Graph

An undirected network is a set of nodes, \(\nu = \{\nu_1, \nu_2, \ldots, \nu_N\}\), and a set of edges, \(\epsilon = \{\epsilon_1, \epsilon_2, \ldots, \epsilon_K\}\), for \(K, N \in \mathbb{N}\) such that each edge in \(\epsilon\) connects an element in \(\nu\) to another (not necessarily distinct) element of \(\nu\).

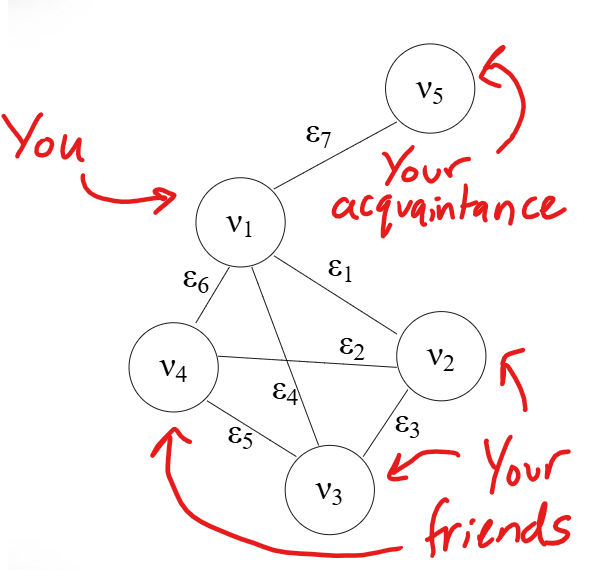
We will also reconsider our second example from the first post:

Figure 1: A simple graph of the network between you, your friend group, and an acquaintance of yours.

Another important measure of connectivity is the node degree of a given node within a network. A formal definition of the node degree can be found below.

Definition 2: Node Degree

Given an undirected network, \(G = \left\{ \nu, \epsilon \right\}\), with $N$ nodes (as in Definition 1), the node degree of a given node \(\nu_i\) can be defined by the adjacency matrix:

\[\begin{equation} \text{deg}(\nu_i) = \sum_{j = 1}^{N} A_{ij} \end{equation}\]

for integer \(i \in \left\{1, \ldots, N \right\}\)

One can think of the node degree as the number of connections that the node in question has. This can be a useful quantifier of a person’s popularity or a measure of how accessible an area is by transport links.

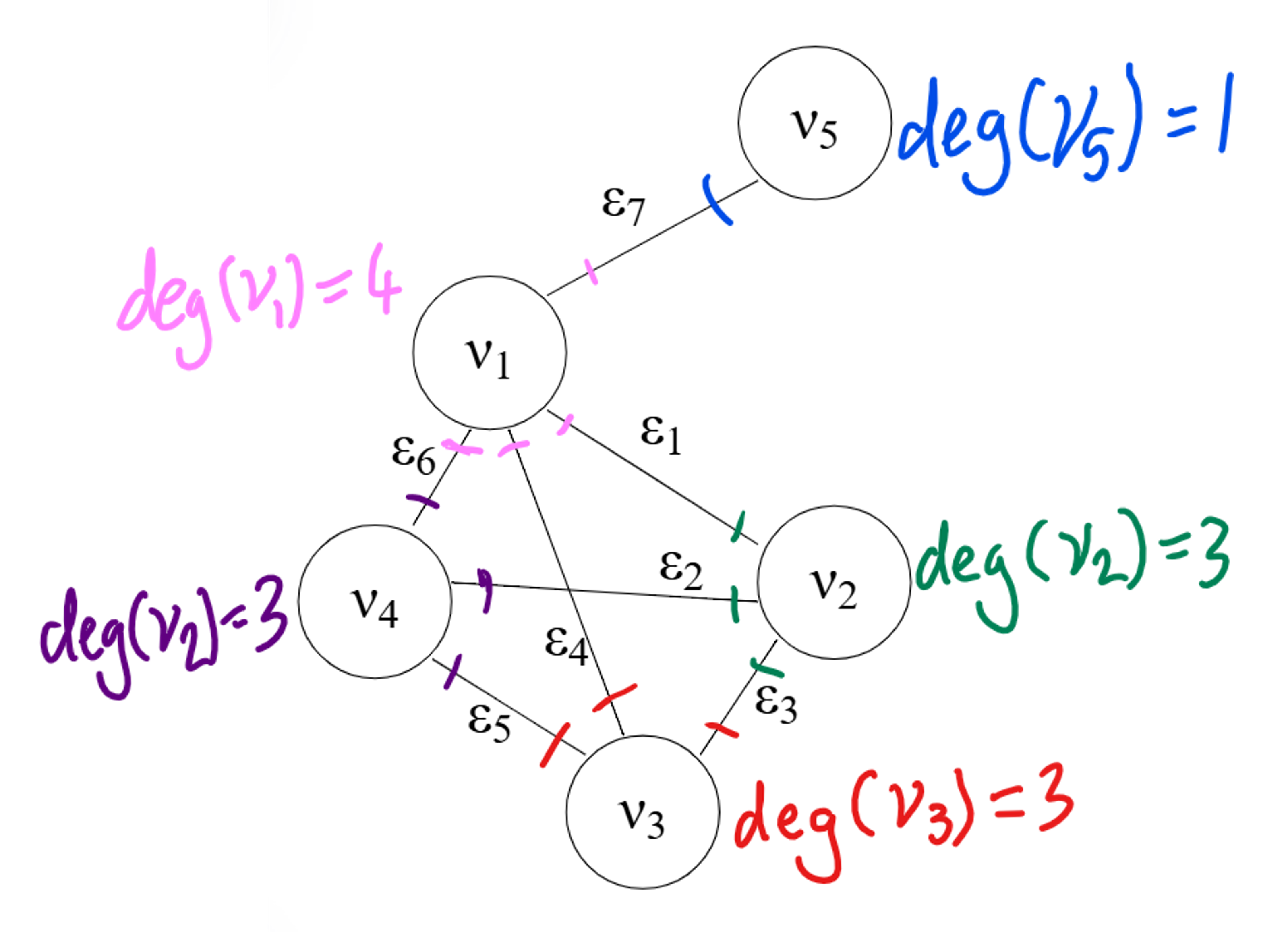
In the network portrayed in Figure 1, we can count the node degree by either using the adjacency matrix or by counting how many edges are attached to each node. Check that you can do this by confirming my results below with the graph in Figure 1:

\[\begin{align}\text{deg}(\nu_1) &= A_{11} + A_{12} + A_{13} + A_{14} + A_{15} \\ &= 0 + 1 + 1 + 1 + 1 \\ &= 4 \end{align}\] \[\begin{align}\text{deg}(\nu_2) &= A_{21} + A_{22} + A_{23} + A_{24} + A_{25} \\ &= 1 + 0 + 1 + 1 + 0 \\ &= 3 \end{align}\] \[\begin{align}\text{deg}(\nu_3) &= A_{31} + A_{32} + A_{33} + A_{34} + A_{35} \\ &= 1 + 1 + 0 + 1 + 0 \\ &= 3 \end{align}\] \[\begin{align}\text{deg}(\nu_4) &= A_{41} + A_{42} + A_{43} + A_{44} + A_{45} \\ &= 1 + 1 + 1 + 0 + 0 \\ &= 3 \end{align}\] \[\begin{align}\text{deg}(\nu_5) &= A_{51} + A_{52} + A_{53} + A_{54} + A_{55} \\ &= 1 + 0 + 0 + 0 + 0 \\ &= 1 \end{align}\]

This tells us that node \(\nu_1\) has the highest node degree and is therefore the most connected node in this network.

If you are given the graph of a network, you can count the degree of each node by counting the edges which are incident to it. See an annotated version of Figure 1 below, where I count the edges which are incident to each node, determing the degree of each node.

Figure 2: An annotated graph to show the process of counting edges to determine the node degree of each node.