1.2 Incidence matrix

Recall, our definition of an undirected graph.

Definition 1: Undirected Graph

An undirected network is a set of nodes, \(\nu = \{\nu_1, \nu_2, \ldots, \nu_N\}\), and a set of edges, \(\epsilon = \{\epsilon_1, \epsilon_2, \ldots, \epsilon_K\}\), for \(K, N \in \mathbb{N}\) such that each edge in \(\epsilon\) connects an element in \(\nu\) to another (not necessarily distinct) element of \(\nu\).

We will also reconsider our second example from the first post:

Figure 1: A simple graph of the network between you, your friend group, and an acquaintance of yours.

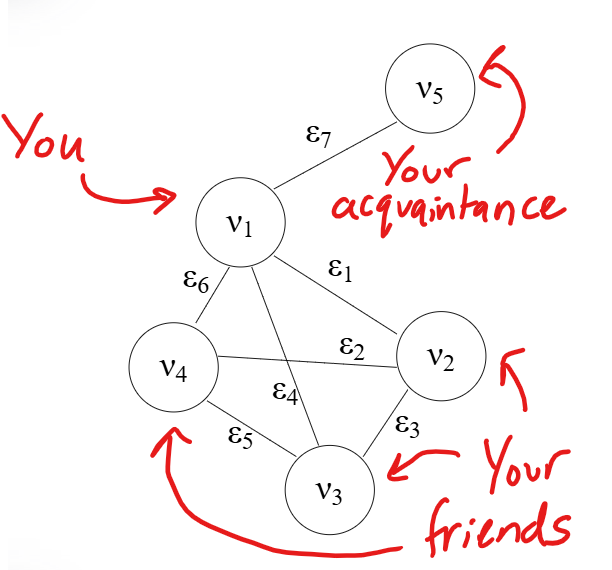
We may wish to consider the connectivity of a graph from the perspective of its edges. This is known as the incidence matrix; a way of capturing how each node is incident (connected) to each edge.

Definition 2: Incidence Matrix

Given an undirected network (as in Definition 1), the incidence matrix, \(E\), is defined as an \(N \times K\) matrix where:

\[\begin{equation} E_{ij} = \begin{cases} 1 \text{ if } \nu_i \in \epsilon_j\\ 0 \text{ if } \nu_i \notin \epsilon_j\ \end{cases} \end{equation}\]

for integers \(i \in \left\{1, \ldots, N \right\}\) and \(j \in \left\{1, \ldots, K \right\}\)

If we consider the graph in Figure 1, one can create its incidence matrix:

\[E = \begin{pmatrix} 1 & 0 & 0 & 1& 0 & 1& 1 \\ 1 & 1 & 1 & 0& 0 & 0 & 0\\ 0 & 0 & 1 & 1& 1 & 0 & 0\\ 0 & 1 & 0 & 0& 1 & 1 & 0\\ 0 & 0& 0 & 0& 0 & 0 & 1\\ \end{pmatrix}\]

To see this a bit more clearly, I have annotated which edge is incident to each node by labelling the columns and rows respectively.

Figure 2: An incidence matrix, annotated.

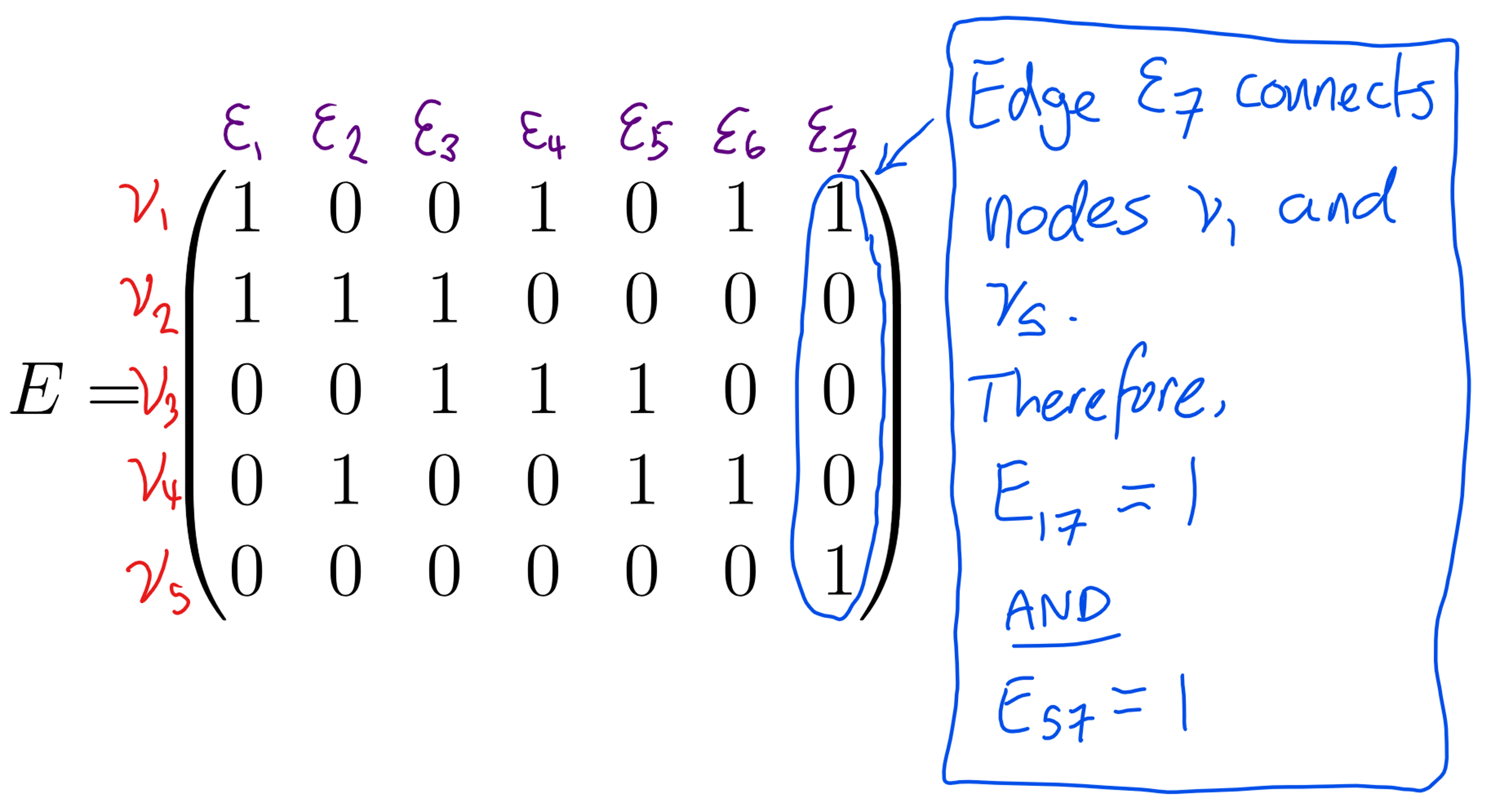
This is an alternative way to portray the connectivity of the network and becomes very useful if your focus is on the edges between specific units. In transport networks, the edges are often the primary focal points of investigation.