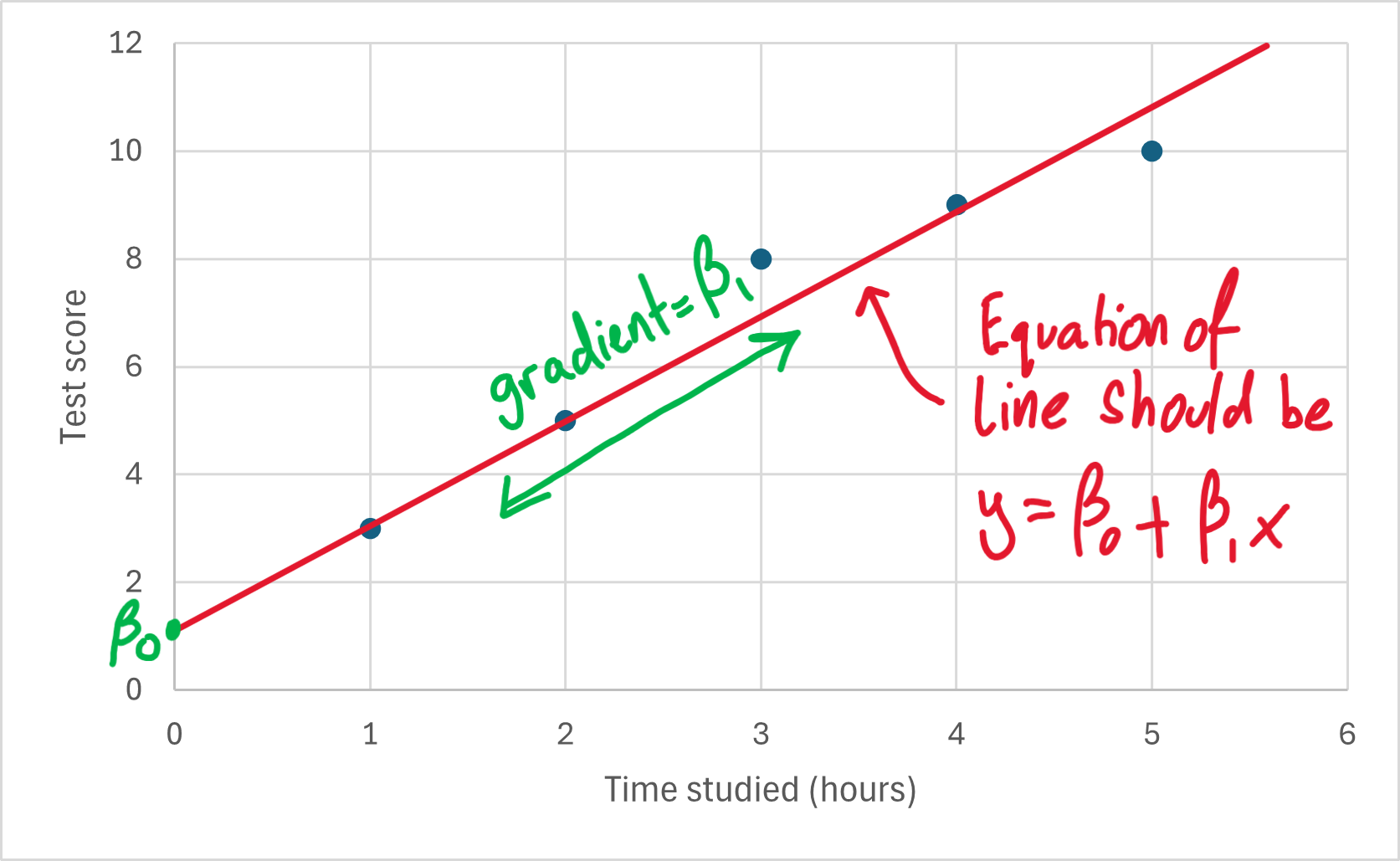
1.0 Simple Linear Regression
An introduction to simple linear regression; an approach to model a relationship between values of an independent variable and values of a dependent variable.
Design of Experiments
I am currently in the process of putting some notes together on experimental design. Please do let me know your thoughts or improvements either via X / Twitter or LinkedIn. I hope these notes are useful!
- Dan
§1 An Introduction to Regression
Though not strictly under the guise of experimental design, regression provides a solid introduction to much of the analysis that we conduct in experimental design - particularly when discussing optimal designs.
I thought that this would be a good place to start, since no experimental design knowledge is required to understand regression.
1.1 Estimating `β_0` and `β_1` using least squares estimation
We shall introduce least squares estimation as a means to estimate `β_0` and `β_1`.
1.2 Introduction to non-linear polynomial regression
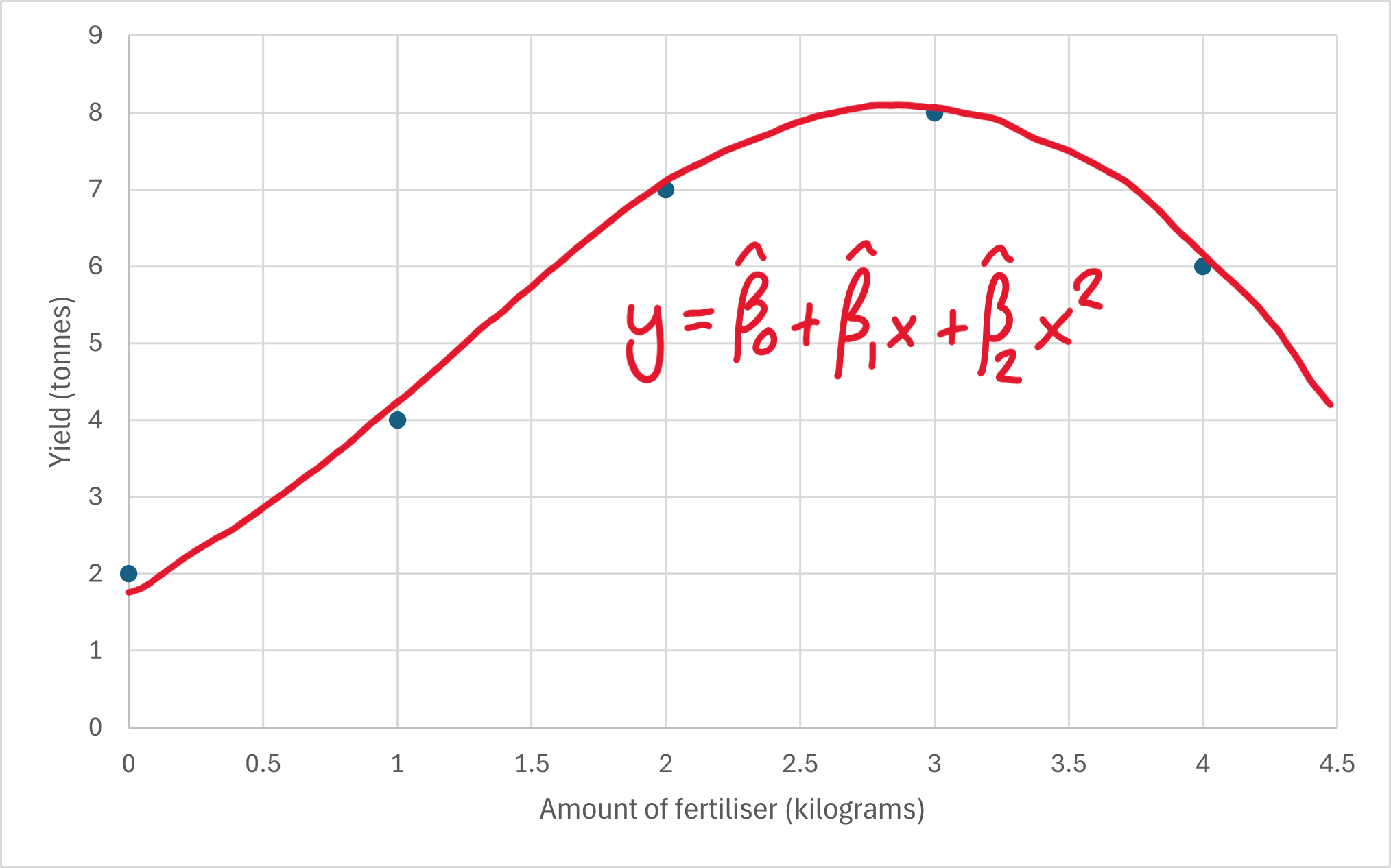
Extending our understanding of linear regression to the quadratic case.
1.3 Determining the Precision of Estimating `β_j`
We shall introduce how we determine how precise our estimators are.
§3 An Introduction to Design Optimality
I am aiming to provide a formal introduction to experimental design in the future (see the currently missing §2). For now, and for the purposes of my studies, I wish to make notes on optimality. I believe this follows on nicely from our discussions of the design matrix in the first section. Much of design optimisation theory relies on minimising the variance of the estimator(s) in some form.
3.0 What is experimental design optimality?
We shall introduce the concept of optimality in the context of experimental design and discuss its importance.
3.1 `D`-Optimality Introduction
Exploring `D`-optimality and how it dictates a solid experiment.
3.2 `A`-Optimality Introduction
Exploring `A`-optimality and how it asserts a solid experiment.
3.3 `E`-Optimality Introduction
Exploring `E`-optimality and how it explains a solid experiment.
3.4 `T`-Optimality Introduction
Exploring `T`-optimality and how it tells whether we have a solid experiment.
3.5 `G`-Optimality Introduction
Exploring `G`-optimality and how it governs a solid experiment.