1.1 Adjacency matrix

Recall, our definition of an undirected graph.

Definition 1: Undirected Graph

An undirected network is a set of nodes, \(\nu = \{\nu_1, \nu_2, \ldots, \nu_N\}\), and a set of edges, \(\epsilon = \{\epsilon_1, \epsilon_2, \ldots, \epsilon_K\}\), for \(K, N \in \mathbb{N}\) such that each edge in \(\epsilon\) connects an element in \(\nu\) to another (not necessarily distinct) element of \(\nu\).

We will also reconsider our second example from the first post:

Figure 1: A simple graph of the network between you, your friend group, and an acquaintance of yours.

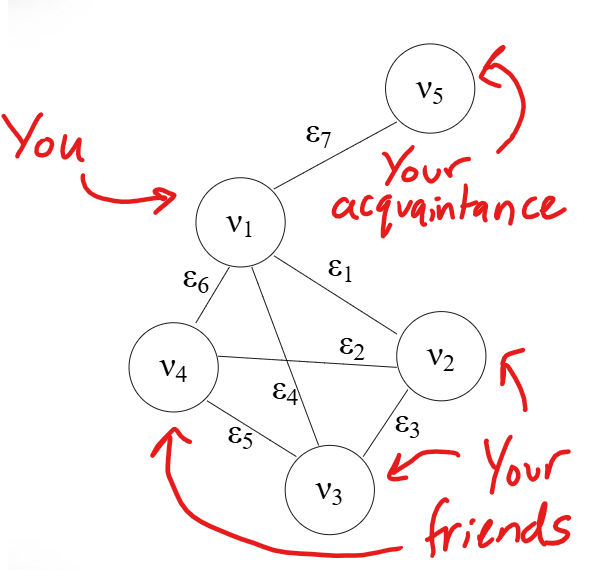
It is almost always important to consider the connectivity of nodes. This is where the real magic of networks reveals itself. Fortunately, there is a super legible way to convey the interconnectivity of nodes - this is known as the adjacency matrix.

Adjacency matrix

The adjacency matrix tells us what nodes are connected to each node in a legible format.

Definition 2: Adjacency Matrix

Given an undirected network (as in Definition 1), the adjacency matrix, \(A\), is defined as a symmetric \(N \times N\) matrix where:

\[\begin{equation} A_{ij} = \begin{cases} 1 & \text{if } (i, j) \in \epsilon \\ 0 & \text{if } (i, j) \notin \epsilon \end{cases} \end{equation}\]

for integers \(i, j \in \left\{1, \ldots, N \right\}\)

From this definition, one can see that there is a \(1\) in the \(ij\)-th element of the adjacency matrix if nodes \(\nu_i\) and \(\nu_j\) are connected.

As an example, consider the graph in Figure 1. One can create its adjacency matrix:

\[A = \begin{pmatrix} 0 & 1 & 1 & 1 & 1 \\ 1 & 0 & 1 & 1 & 0 \\ 1 & 1 & 0 & 1 & 0 \\ 1 & 1 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ \end{pmatrix}\]

To see this a bit more clearly, I have annotated which node is connected to each node by labelling the rows and columns of the above adjacency matrix.

Figure 2: An adjacency matrix, annotated.

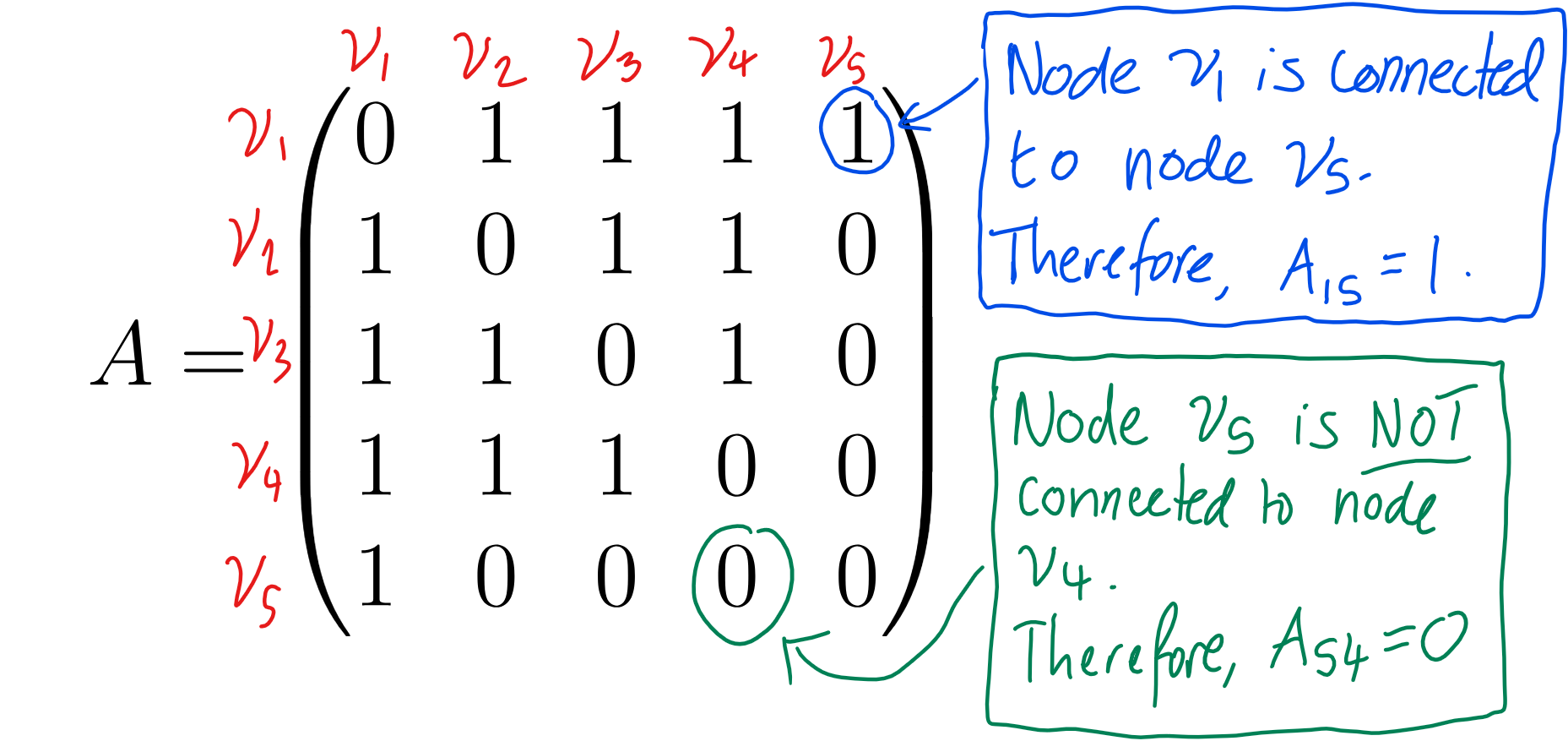
As you can see, in congruence with Figure 1, everybody knows everybody in your friend group, and your acquaintance is only known by you. The adjacency matrix allows us to represent the connectivity of a given network without having to draw the graph. It is easy to imagine that drawing a graph with a large number of nodes and/or edges can become quite a headache.

Question 1

Consider an undirected graph with node set

\[\nu = \left\{1, 2, 3\right\}\]

and edge set

\[\epsilon = \left\{(1, 2), (1, 3), (2, 3)\right\}\]

Construct the adjacency matrix for this graph.

Firstly, list the nodes: 1, 2, 3. Then, we shall set up an empty adjacency matrix. The matrix will have a size of 3x3 (since there are 3 nodes). $$A = \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{pmatrix}$$ For each edge, place a 1 in the corresponding row and column. We know that nodes 1 and 2 are connected. Hence, $$A = \begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \\ \end{pmatrix}$$ Now, fill in the rest of the matrix by reading across the edge list. You should end up with this: $$A = \begin{pmatrix} 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\ \end{pmatrix}$$ This matrix represents the connections between nodes in the graph. Each 1 indicates an edge between two nodes, while 0 indicates no edge. Notice the symmetry here - this is a direct consequence of the graph being undirected. We shall explore what undirected means in the next chapter.

Question 2

Consider an undirected graph with node set

\[\nu = \left\{1, 2, 3, 4\right\}\]

and edge set

\[\epsilon = \left\{(1, 2), (1, 3), (2, 4), (3, 4), (3, 2)\right\}\]

Construct the adjacency matrix for this graph.

Firstly, list the nodes: 1, 2, 3, 4. Then, we shall set up an empty adjacency matrix. The matrix will have a size of 4x4 (since there are 4 nodes). $$A = \begin{pmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{pmatrix}$$ For each edge, place a 1 in the corresponding row and column. We know that nodes 1 and 2 are connected. Hence, $$A = \begin{pmatrix} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{pmatrix}$$ Now, fill in the rest of the matrix by reading across the edge list. You should end up with this: $$ A = \begin{pmatrix} 0 & 1& 1 &0 \\ 1 &0 &1 &1 \\ 1 &1 &0 &1 \\ 0 &1 &1 &0 \\ \end{pmatrix}$$ This matrix represents the connections between nodes in the graph. Each 1 indicates an edge between two nodes, while 0 indicates no edge.